|
Tutorial 1 Binary numbering system Objective: The objective of this tutorial is to
learn how the binary numbering system works. The student will be able to: 1.
Differentiate
between various numbering systems, such as decimal, binary, octal, and
hexadecimal 2.
Convert a
binary number to its decimal equivalent Numbering system is a way of representing numbers. ·
The most
common is the decimal numbering system. It is called base 10, because it has
10 digits ·
There are
other numbering systems as well, such as Octal, hexadecimal and binary
numbering. ·
Each number
system has a base. In the octal system, there can be eight
possibilities:
In the decimal system, there are ten numbers:
In the hexadecimal system, we use 16 numbers: 0-9
and A-F
To
convert a binary number to its decimal equivalent In
order to convert a binary to its decimal equivalent we need to know a few
things: ·
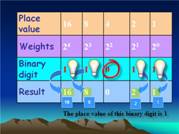
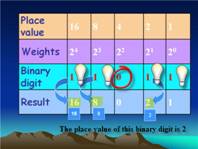
Its place
value or position value ·
Its weight or
the exponent value and ·
Its status in
terms of whether the binary digit is a 0 or a 1 The
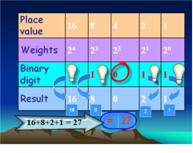
following pictures will show the step by-step approach to convert a binary
number 11011 to its decimal equivalent.
The
final value will be 27: Exercises: Using
the above table, convert the following binary digits into their decimal
equivalent: 1.
110010 2.
1010111 3.
111111 4.
001100 5.
010101 Check
your answers with this Binary Converter |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|